Moviment Brownjan

Il-moviment Brownjan ta' partiċella

Il- moviment Brownjan hu deskrizzjoni matematika ta' moviment każwali ta' partiċella "tqila" mgħaddsa fi fluwidu u li m'għandhiex fuqha interazzjonijiet oħra ħlief il-ħbit fuqha tal-molekuli "ħfief" tal-fluwidu ta' madwarha. Minn dan jirriżulta li l-partiċella t-tqila timxi b'moviment irregolari ħafna, li ġie deskritt għall-ewwel darba fl-1827 mill-botanista Robert Brown waqt li kien qiegħed josserva ċ-ċaqlieq ta' partiċelli fil-fluwidu fil-ġewwieni ta' trab tal-pollin.

Id-deskrizzjoni fiżika l-iżjed elementari ta' dan il-fenomenu hi din:

• bejn żewġ ħabtiet, il-partiċella l-kbira timxi f'linja dritta b'veloċità kostanti;
• il-partiċella l-kbira taċċelera meta taħbat ma' molekula tal-fluwidu jew xi ħajt.

Permezz ta' dan il-moviment nistgħu niddeskrivu l-imġiba termodinamika tal-gasijiet (teorija ċinetika tal-gasijiet), kif ukoll il-fenomenu tad-diffużjoni. Huwa użat ħafna wkoll fil-mudelli tal-matematika finanzjarja.

Ħjiel storiku

Brown ra fil-fluwidu li kien fil-ġewwieni tat-trab tal-pollin (il-moviment Brownjan ma ġiex osservat fuq it-trab tal-pollin stess kif jingħad sikwit), xi partiċelli żgħar ħafna jiċċaqilqu b'movimenti li kienu jidhru kaotiċi. Dan ma setax jiġi spjegat permezz ta' kurrenti u lanqas permezz ta' xi fenomenu fiżiku ieħor magħruf. Għall-ewwel Brown għalhekk attribwieh għal xi attività ħajja. L-ispjegazzjoni korretta tal-fenomenu ġiet wara.

Brown ma kienx eżattament l-ewwel wieħed li għamel din l-osservazzjoni. Qal hu stess li bosta oħrajn kienu ssuġġerew l-eżistenza ta' dan il-moviment (f'konnessjoni mat-teoriji vitalisti ta' żmienu). Nistgħu insemmu lill-qasis kattoliku John Turberville Needham (1713-1781), famus f'ħajtu għas-sengħa li kellu fuq il-mikroskopju, u lill-Olandiż Jan Ingenhousz (1730 -1799) li fl-1785 iddeskriva l-moviment irregolari tat-trab tal-faħam fuq wiċċ l-alkoħol.

Matul is-seklu 20 kien hemm ħafna diskussjonijiet dwar x'kien osserva sewwa Brown. Minħabba l-kwalità medjokra tal-apparat li seta' jinqeda bih, xi wħud iddubitaw jekk kienx veru li ra l-moviment Brownjan, li kien jinvolvi partiċelli ta' xi mikrometri mill-iżjed. L-Ingliż Brian Ford reġa' għamel l-esperiment fil-bidu tas-snin 1990, bil-materjal użat minn Brown u f'kondizzjonijietet li kienu l-istess kemm jista' jkun. Il-moviment kien veru osservat f'dawn il-kondizzjonijiet u hekk ġew ikkonfermati l-osservazzjonijiet ta' Brown.

Rudimenti matematiċi

Il-kunċett ta' proċess każwali

Insibuh diffiċli li nimmudellaw il-moviment Brownjan minnħabba l-fatt li dan il-moviment hu każwali u li statistikament kull partiċella ma timxix: mhuwiex moviment tal-partiċelli kollha f'daqqa bħar-riħ jew kurrent. Iżjed preċiż:

• f'waqt mogħti, is-somma vettorjali tal-veloċitajiet tal-partiċelli hi żero (m'hemmx moviment tal-ġabra tal-partiċelli);
• jekk insegwu partiċella mogħtija, matul iż-żmien, il-bariċentru tal-mogħdija tagħha hu l-punt minn fejn tkun telqet, tagħmel "dawra durella" madwar l-istess punt.

Hu diffiċli f'dawn il-kondizzjonijiet li nikkaratterizzaw il-moviment. Is-soluzzjoni sabha Louis Bachelier, u ppreżentaha fit-teżi tiegħu li ddefenda fid-29 ta' Marzu 1900. Wera li dak li jikkaratterizza l-moviment, m'hijiex il-medja aritmetika tal-pożizzjonijiet $\langle X\rangle$ imma l-medja kwadrata ${\sqrt {\langle \,X^{2}\,\rangle \ }}$ : jekk $\ x(t)$ hi d-distanza tal-partiċella fil-ħin $\ t$ wara li telqet minn fejn telqet, allura :

$\langle \,X^{2}(t)\ \rangle \ =\ {\frac {1}{t}}\int _{0}^{t}x^{2}(\tau )\ d\tau$

Nistgħu nuru li hawn l-ispostament kwadrat medju hu proporzjonali għall-ħin :

$\langle \,X^{2}(t)\ \rangle \ =\ 2\,d\,D\,t$

fejn $\ d$ hi d-dimensjoni tal-moviment (linjari, pjan, spazjali), $\ D$ il-koeffiċjent tad-diffużjoni u $\ t$ il-ħin li jkun għadda.

Definizzjoni matematika

Nistgħu nagħtu din id-definizzjoni formali: Il-moviment Brownjan hu proċess stokastiku $(B_{t})_{(t\geq 0)}$ fejn l-inkrementi disġunti huma indipendenti u l-inkrement $\ B_{t+s}-B_{t}$ jobdi l-liġi normali b'medja żero u varjanza $\ s$.

Permezz ta' din id-definizzjoni nistgħu nippruvaw xi proprjetajiet tal-moviment Brownjan, bħal pereżempju il-kontinwità tiegħu (kważi żgura), il-fatt li kważi żgurament, il-mogħdija tiegħu m'hi mkien differenzjabbli, u bosta proprjetajiet oħra.

Nistgħu ukoll niddefinixxu l-moviment Brownjan permezz tal-varjanza. Din id-definizzjoni, imsejħa t-teorema ta' Lévy, tagħti din il-karatterizzazzjoni: Proċess stokastiku li hu martingala lokali u għandu varjanza $\ t$ hu moviment Brownjan.

Il-formola ta' Einstein

Permezz tal-formola li tajna hawn fuq nistgħu nikkalkulaw il-koeffiċjent tad-diffużjoni ta' par partiċella-fluwidu. Ġaladarba nkunu nafu l-karatteristiċi tal-partiċella li qiegħda tiddifuża, nistgħu niddeduċu l-karatteristiċi tal-ieħor. Jekk inkunu nafu l-karatteristiċi tat-tnejn, inkunu nistgħu nikkalkulaw in-numru ta' Avogadro bl-għajnuna tal-formola ta' Einstein (1905) :

$D\ =\ {\frac {RT}{6\pi \eta {\mathcal {N}}_{Av}r}}$

fejn $\ R$ hi l-kostanti tal-gasijiet perfetti, $\ T$ it-temperatura, $\ \eta$ il- viskożità tal-fluwidu, $\ r$ ir-raġġ tal-partiċella u ${\mathcal {N}}_{Av}$ in-numru ta' Avogadro. Il-fiżiku Jean Perrin ikkalkula dan in-numru fl-1908 permezz ta' din il-formola.

Xi mudelli fl-spazju Ewklidew

L-ekwazzjoni ta' Langevin (1908)

Fil-metodu ta' Langevin, il-partiċella Brownjana l-kbira ta' massa $\ m$ għandha fil-waqt $\ t$, veloċità $\ v(t)$ u jaħkmu fuqha żewġ forzi:

• forza ta' frizzjoni fluwida tat-tip $f\,=\,-\,k\,v$, fejn $\ k$ hi kostanti pożittiva;
• ħoss abjad Gaussjan, $\ \eta$.

Meta napplikaw il-prinċipju fundamentali tad-dinamika ta' Newton b'dawn il-forzi niksbu l-ekwazzjoni stokastika ta' Langevin:

$m\,{\frac {dv(t)}{dt}}\ =\ -\,k\,v(t)\ +\ \eta (t)$

Il-proċess ta' Ornstein-Uhlenbeck

Il-proċess ta' Ornstein-Uhlenbeck hu proċess stokastiku li jiddeskrivi l-veloċita ta' partiċella fi fluwidu, f'dimensjoni 1.

Niddefinuh bħala s-soluzzjoni $\ X_{t}$ ta' din l-ekwazzjoni differenzjali stokastika:

$dX_{t}={\sqrt {2}}dB_{t}-X_{t}dt$,

fejn $\ B_{t}$ hu moviment Brownjan standard, u $\ X_{0}$ hi varjabbli każwali mogħtija. It-terminu $\ dB_{t}$ jirrappreżenta l-għadd kbir ta' ħabtiet stokastiċi mal-partiċella, waqt li t-terminu $\ -{X_{t}}dt$ jirrappreżenta l-forza tal-frizzjoni fuq il-partiċella.

Il-formola ta' Itô applikata għall-proċess $\ {e^{t}}X_{t}$ tagħtina:

$d({e^{t}}X_{t})={e^{t}}{X_{t}}dt+{e^{t}}({\sqrt {2}}{dB_{t}}-{X_{t}}dt)={e^{t}}{\sqrt {2}}{dB_{t}}$,

li fil-forma integrali ssir:

$X_{t}={X_{0}}e^{-t}+{\sqrt {2}}e^{-t}\int _{0}^{t}{e^{s}}dB_{s}$.

Pereżempju, jekk $\ X_{0}$ tieħu kważi żgur il-valur $\ x$, Il-liġi ta' $\ X_{t}$ hi liġi Gaussjana b'medja $\ xe^{-t}$ u varjanza $\ 1-e^{-2t}$, li tikkonverġi fil-liġi meta $\ t$ tersaq lejn l-infinit għal liġi Gaussjana standard.

Mixjiet każwali

Nistgħu nużaw mudell ta' mixja każwali, fejn il-moviment isir b'qabziet diskreti bejn pożizzjonijiet fissi (b'movimenti f'linja dritta bejn żewġ pożizzjonijiet), bħal pereżempju fil-każ tad-diffużjoni fis-solidi. Jekk ix-$\ X_{i}$ huma l-pożizzjonijiet wara xulxin ta' partiċella, wara $\ n$ qabżiet ikollna:

$\langle \,X_{n}^{2}\ \rangle \ =\ {\frac {1}{n}}\ \sum _{i=1}^{n}\ x_{i}^{2}.$

Mixja każwali f'dimensjoni waħda tal-ispazju (Eżempju)

Ejjew inħarsu lejn mixja ta' partiċella fuq l-assi Ox. Nissoponu li din il-partiċella tagħmel qabżiet ta' tul $\ a$ bejn pożizzjonijiet ġirien ta' xulxin sitwati fuq l-għoqod tax-xibka: $\{\,n\,a\ ,n\in \mathbb {Z} \,\}$ ta' ħadma $\ a$ u kull qabża ddum żmien $\ \tau$.

Irridu nagħtu wkoll numru $\ p$ li jissodisfa: $\ 0<p<1$. L-interpretazzjoni fiżika ta dan il-parametru hi din:

• $\ p$ tirrapreżenta l-probabbiltà li l-partiċella taqbeż lejn il-lemin kull darba;
• $\ q=1-p$ tirrapreżenta l-probabbiltà li l-partiċella taqbeż lejn ix-xellug kull darba.

Il-każ tal-moviment Brownjan jikkorrispondi ma' li nagħmlu l-ipoteżi ta' iżotropija spazjali. Id-direzzjonijiet fl-ispazju fiżiku huma a priori ekwivalenti u l-probabbiltajiet ta' qbiż lejn iż-żewġ direzzjonijiet huma l-istess:

$p\ =\ q\ =\ {\frac {1}{2}}$

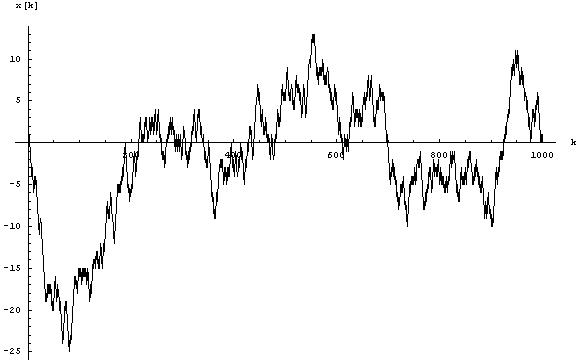
Ix-xbieha hawn taħt turi eżempju tipiku tar-riżultat: il-partiċella titlaq minn $\ 0$, $\ x(0)=0$, u l-linja timxi mal-pożizzjonijiet suċċessivi $\ x(k)$ tal-partiċella fil-ħinijiet $\ k$.

Il-probabbiltà ta' tranżizzjoni kondizzjonali

Il-probabbiltà ta' tranżizzjoni kondizzjonali niddefinuha hekk:

$P(n|m,s)\ =\ P(na|ma,s\tau )$

bħala l-probabbiltà li nsibu l-partiċella fuq is-sit (għoqda) $\ ma$ fil-ħin $\ s\tau$ meta nkunu nafu li kienet fuq is-sit $\ na$ fil-ħin tal-bidu $\ 0$.

L-ipoteżi ta' iżotropija twassalna biex niktbu l-liġi tal-evoluzzjoni ta' din il-pobabbiltà ta' tranżizzjoni kondizzjonali b'dan il-mod :

$P(n|m,s+1)\ =\ {\frac {1}{2}}\ \left[\ P(n|m+1,s)\ +\ P(n|m-1,s)\ \right]$

Minnha niddeduċu din ir-relazzjoni:

$P(n|m,s+1)\,-\,P(n|m,s)\ =\ {\frac {1}{2}}\ \left[\ P(n|m+1,s)\,+\,P(n|m-1,s)\,-\,2\ P(n|m,s)\ \right]$

Konverġenza lejn il-moviment Brownjan. Ekwazzjoni ta' Fokker-Planck

Ejjew nieħdu l-limitu kontinwu tal-aħħar ekwazzjoni, jiġifieri nieħdu l-limitu bil-parametri:

• $\tau \ \to \ 0$

• $a\ \to \ 0$

Meta nagħmlu l-kalkulu tal-limitu kontinwu naraw li l-kumbinazzjoni $\ a^{2}/2\tau$ trid tibqa' kostanti f'dan il-limitu. Meta niżviluppaw $\ P$ f'poteri ta' $\ \tau$ insibu:

$P(n|m,(s+1)\tau )\ -\ P(n|m,s\tau )\ =\ \tau D_{2}P(n|m,s\tau )+\ O(\tau ^{2}).$

Meta niżviluppawha f’poteri ta' $\ a$ ikollna:

$P(n|(m\pm 1)a,s)\ =\ P(n|ma,s)\,\pm \,a\tau D_{1}P(n|ma,s)+\,{\frac {a^{2}}{2}}\tau D_{1}^{2}P(n|ma,s)+\,O(a^{3}).$

u jekk nagħqduhom dawn tal-aħħar flimkien inġibu:

$P(n|m+1,s)\,+\,P(n|m-1,s)\,-\,2\ P(n|m,s)\ =\ a^{2}\tau D_{1}^{2}P(n|ma,s)+\,O(a^{3}).$

Minn dawn nistgħu niddeduċu l-ekwazzjoni ta' Fokker-Planck :

$\tau \ D_{2}P(x_{0}|x,t)\ =\ {\frac {a^{2}}{2}}\ D_{1}^{2}P(x_{0}|x,t),$

jew

$\tau \ {\frac {\partial P(x_{0}|x,t)}{\partial t}}\ =\ {\frac {a^{2}}{2}}\ {\frac {\partial ^{2}P(x_{0}|x,t)}{\partial x^{2}}}$

li nistgħu nerġgħu niktbuha:

${\frac {\partial P(x_{0}|x,t)}{\partial t}}\ =\ D\ {\frac {\partial ^{2}P(x_{0}|x,t)}{\partial x^{2}}}$

meta nintroduċu l-koeffiċjent tad-diffużjoni:

$D\ =\ {\frac {a^{2}}{2\tau }}.$

Solution tal-ekwazzjoni ta' Fokker-Planck

Barra mill-ekwazzjoni ta' Fokker-Planck, id-densità ta' probabbiltà ta' tranżizzjoni kondizzjonali $\ P(x_{0}|x,t)$ trid tissosdisfa iż-żewġ kondizzjonijiet supplementari li ġejjin:

• in-normalizzazzjoni tal-probabbiltà totali:

$\forall \ t\ >\ 0\ ,\quad \int _{-\infty }^{+\infty }dx\ P(x_{0}|x,t)\ =\ 1$

• il-kondizzjoni inizjali:

$\lim _{t\to 0}P(x_{0}|x,t)\ =\ \delta (x-x_{0})$

fejn $\ \delta (x)$ hi d-distribuzzjoi ta' Dirac.

Id-densità ta' probabbiltà ta' tranżizzjoni kondizzjonali $\ P(x_{0}|x,t)$ hi mela essenzjalment funzjoni ta' Green tal-ekwazzjoni ta' Fokker-Planck. Nistgħu nuru li din tinkiteb espliċament:

$P(x_{0}|x,t)\ =\ {\frac {1}{\sqrt {4\pi Dt}}}\ \exp \,\left[\ -\ {\frac {(x-x_{0})^{2}}{4Dt}}\ \right]$

Il-mumenti ta' din id-distribuzzjoni nistgħu nikkalkulawhom faċilment.

Il-moviment Brownjan fuq varjetà Riemannjana

Insejħu moviment Brownjan fuq varjetà Riemannjana $\ V$ il-proċess każwali kontinwu Markovjan li s-semigrupp tiegħu tat-tranżizzjoni b'parametru wieħed hu mnissel minn $\ 1/2\,\Delta _{V}$, fejn $\ \Delta _{V}$ hu l-operatur ta' Laplace-Beltrami fuq il-varjetà $\ V$.

Bibljografija

Aspetti storiċi

• Jean Perrin, Mouvement brownien et réalité moléculaire, (Il-moviment Brownjan u r-realtà molekulari) Annales de Chimie et de Physique 19 (it-8 serje), (1909), 5-104. Wieħed jista' jikkonsulta u jniżżel it-test komplut fil-format pdf minn fuq is-sit Gallica tal-BNF.
• Albert Einstein, Investigations on the Theory of the Brownian Movement, (Starriġ dwar it-teorija tal-moviment Brownjan) Dover Publications, Inc. (1985), ISBN 0-486-60304-0. Edizzjoni mill-ġdid tal-artikli oriġinali ta' Einstein fuq it-teorija tal-moviment Brownjan.

Il-moviment Brownjan fl-ispazju Ewklidew

• Bertrand Duplantier ; Le mouvement brownien, (Il-moviment Brownjan) Séminaire Poincaré : Einstein, 1905-2005 (Pariġi, 8 ta' April 2005). Test komplut disponibbli fuq [3].
• Bernard Derrida u Eric Brunet, Le mouvement brownien et le théorème de fluctuation-dissipation, (Il-moviment Brownjan u t-teorema ta' flutwazzjoni-dissipazzjoni) f Michèle Leduc & Michel Le Bellac (edituri) ; Einstein aujourd'hui, EDP Sciences (Jannar 2005), ISBN 2-86883-768-9.
• Paul Lévy, Processus stochastiques et mouvement brownien, (Proċessi stokastiċi u l-moviment Brownjan) Gauthier-Villars (it-2 edizzjoni - 1965). Re-editjata minn Jacques Gabay (1992), ISBN 2-87647-091-8.
• Mark Kac, Random Walk and the Theory of Brownian Motion, (Mixjiet każwali u t-teorija tal-moviment Brownjan) American Mathematical Monthly 54(7) (1947), 369-391. Test jista' jinstab fil-format pdf fuq [4].
• Edward Nelson, Dynamical Theories of Brownian Motion, (Teoriji dinamiċi tal-moviment Brownjan) Princeton University Press (1967). Test jista' jinstab fil-format pdf fuq [5].

Il-moviment Brownjan fuq varjetà Riemannjana

• Elton P. Hsu ; Stochastic Analysis on Manifolds, (Analisi stokastika fuq il-varjetajiet) American Mathematical Society (Jannar 2002), ISBN 0-8218-0802-8.
• Elton P. Hsu ; A Brief Introduction to Brownian Motion on a Riemannian Manifold, (Introduzzjoni fil-qosor għall-moviment Brownjan fuq varjetà Riemannjana) (2003). Test jista' jinstab fil-format pdf fuq [6].
• Mark A. Pinsky ; Isotropic transport process on a Riemannian manifold, (Proċess iżotropiku tat-trasport fuq varjetà Riemannjana), Transaction of the American Mathematical Society 218 (1976), 353-360.
• Mark A. Pinsky ; Can You Feel the Shape of a Manifold with Brownian Motion ? (Tista' tħoss il-forma ta' varjetà permezz tal-moviment Brownjan ?), Expositiones Mathematicae 2 (1984), 263-271.
• Nicolas Th. Varopoulos ; Brownian motion and random walks on manifolds (Moviment Brownjan u mixjiet każwali fuq varjetajiet), Annales de l'Institut Fourier 34(2) (1984), 243-269. Test jista' jinstab fil-format pdf fuq [7].
• Alexander Grigor'yan ; Analytic and geometric background of recurrence and non-explosion of the Brownian motion on Riemannian manifolds, (Sfond analitiku u ġeometriku tal-moviment Brownjan fuq varjetajiet Riemannjani), Bulletin of the American Mathematical Society 36(2) (1999), 135-249. Test jista' jinstab fuq [8].

Ħoloq esterni

• Animazzjoni bil-Java fuq il-moviment Brownjan (test bl-Inġliż)

Portal Matematika